In the Apr-08-2007 posting, Getting Data Into MATLAB Using textread, basic use of the textread function was explained, and I alluded to code which I used to load the variables names. The name-handling code was not included in that post, and reader Andy asked about it. The code in question appears below, and an explanation follows (apologies for the Web formatting).
% Specify filename
InFilename = 'C:\Data\LA47INTIME.tab';
% Import data from disk
A = textread(InFilename,'','headerlines',1, ...
'delimiter','\t','emptyvalue',NaN,'whitespace','.');
% Establish number of observations ('n') and variables ('m')
[n m] = size(A);
% Note: Load the headers separately because some software
% writes out stupid periods for missing values!!!
% Import headers from disk
FileID = fopen(InFilename); % Open data file
VarLabel = textscan(FileID,'%s',m); % Read column labels
VarLabel = VarLabel{1}; % Extract cell array
fclose(FileID); % Close data file
% Assign variable names
for i = 1:m % Loop over all variables
% Shave off leading and trailing double-quotes
VarLabel{i} = VarLabel{i}(2:end-1);
% Assign index to variable name
eval([VarLabel{i} ' = ' int2str(i) ';']);
end
After the user specifies the data file to be loaded, data is stored in array 'A', whose size is stored in 'n' and 'm'.
Next, the file is re-opened to read in the variable names. Variable names are stored two ways: the actual text names are stored in a cell array, 'VarLabel', and 1 new MATLAB variable is created as an index for each column.
To illustrate, consider a file containing 4 columns of data, "Name", "Sex", "Age" and "Height". The variable 'VarLabel' would contain those 4 names as entries. Assuming that one stores lists of columns as vectors of column indices, then labeling is easy: VarLabel(3) is "Age". This is especially useful when generating series of graphs which need appropriate labels.
Also, four new variables will be created, which index the array 'A'. They are 'Name' (which has a value of 1), 'Sex' (value: 2), 'Age' (3) and 'Height' (4). They make indexing into the main data array easy. The column of ages is: A(:,Age)
I had begun bundling this code as a function, but could not figure out how to assign the variable indices outside of the scope of the function. It is a short piece of code, and readers will likely want to customize some details, anyway. Hopefully, you find this helpful.
Wednesday, March 26, 2008
Sunday, March 23, 2008
A Quick Introduction to Monte-Carlo and Quasi-Monte Carlo Integration
In a surprising range of circumstances, it is necessary to calculate the area or volume of a region. When the region is a simple shape, such as a rectangle or triangle, and its exact dimensions are known, this is easily accomplished through standard geometric formulas. Often in practice, however, the region's shape is irregular and perhaps of very high dimension. Some regions used in financial net present value calculations, for instance, may lie in spaces defined by hundreds of dimensions!
One method for estimating the areas of such regions is Monte Carlo integration. This is a conceptually simple, but very effective solution for some difficult problems. The basic idea is to sample over a region of known area, checking whether sampled points are within the region of interest or not. The proportion of sampled points found to lie within the region of interest multiplied by the (already known) area of the sampled region is an approximation of the area occupied by the region of interest. A related technique, Quasi-Monte Carlo integration, utilizes quasirandom ("low discrepancy") numbers in place of random ones.
An Example
To illustrate Monte Carlo integration, consider a problem with a known analytical solution: calculating the area of a circle. Suppose our circle lies within the unit square, ranging from 0.0 to 1.0 on both dimensions. This circle's center is at (0.5,0.5) and has a radius of 0.5. By the well-known formula, area of a circle = pi * radius squared, this circle has an area of:
>> pi * (0.5 ^ 2)
ans =
0.7854
Using MATLAB to approximate this measurement using Monte Carlo, we have:
>> n = 1e5; % Set number of samples to draw
>> rand('twister',9949902); % Initialize pseudorandom number generator
>> A = rand(n,2); % Draw indicated number of 2-dimensional coordinates in unit square
>> AA = sqrt(sum((A' - 0.5) .^ 2))' <= 0.5; % Determine whether samples are within circular region of interest
>> mean(AA) % Estimate area of the circle via the Monte Carlo method
ans =
0.7874
So, after one hundred thousand samples we are off by a small amount. Note that in this case, the area of the total sampled region is 1.0, so there's no need to divide. Let's see how well the Quasi-Monte Carlo technique performs:
>> n = 1e5; % Set number of samples to draw
>> HSet = haltonset(2); % Set up the Halton quasirandom process for 2-dimensional samples
>> B = net(HSet,n); % Draw indicated number of samples using quasirandom numbers
>> BB = sqrt(sum((B' - 0.5) .^ 2))' <= 0.5; % Determine whether samples are within circular region of interest
>> mean(BB) % Estimate area of the circle via the quasi-Monte Carlo method
ans =
0.7853
In this instance (and this will be true for many problems), quasirandom numbers have converged faster.
See also the Mar-19-2008 posting, Quasi-Random Numbers. As mentioned in that post, coordinates of a regular grid could be substituted for the random or quasirandom numbers, but this requires knowing in advance how many samples are to be drawn, and does not allow arbitrary amounts of further sampling to be used to improve the approximation.
Naturally, one would never bother with all of this to calculate the area of a circle, given the availability of convenient formula, but Monte Carlo can be used for regions of arbitrary, possibly highly irregular- even disjoint- regions. As with the bootstrap, simulated annealing and genetic algorithms, this method is made possible by the fact that modern computers provide tremendous amounts of rapid, accurate computation at extremely low cost.
Further Reading
For a good overview of the Monte Carlo method, see:
Monte Carlo Method
One method for estimating the areas of such regions is Monte Carlo integration. This is a conceptually simple, but very effective solution for some difficult problems. The basic idea is to sample over a region of known area, checking whether sampled points are within the region of interest or not. The proportion of sampled points found to lie within the region of interest multiplied by the (already known) area of the sampled region is an approximation of the area occupied by the region of interest. A related technique, Quasi-Monte Carlo integration, utilizes quasirandom ("low discrepancy") numbers in place of random ones.
An Example
To illustrate Monte Carlo integration, consider a problem with a known analytical solution: calculating the area of a circle. Suppose our circle lies within the unit square, ranging from 0.0 to 1.0 on both dimensions. This circle's center is at (0.5,0.5) and has a radius of 0.5. By the well-known formula, area of a circle = pi * radius squared, this circle has an area of:
>> pi * (0.5 ^ 2)
ans =
0.7854
Using MATLAB to approximate this measurement using Monte Carlo, we have:
>> n = 1e5; % Set number of samples to draw
>> rand('twister',9949902); % Initialize pseudorandom number generator
>> A = rand(n,2); % Draw indicated number of 2-dimensional coordinates in unit square
>> AA = sqrt(sum((A' - 0.5) .^ 2))' <= 0.5; % Determine whether samples are within circular region of interest
>> mean(AA) % Estimate area of the circle via the Monte Carlo method
ans =
0.7874
So, after one hundred thousand samples we are off by a small amount. Note that in this case, the area of the total sampled region is 1.0, so there's no need to divide. Let's see how well the Quasi-Monte Carlo technique performs:
>> n = 1e5; % Set number of samples to draw
>> HSet = haltonset(2); % Set up the Halton quasirandom process for 2-dimensional samples
>> B = net(HSet,n); % Draw indicated number of samples using quasirandom numbers
>> BB = sqrt(sum((B' - 0.5) .^ 2))' <= 0.5; % Determine whether samples are within circular region of interest
>> mean(BB) % Estimate area of the circle via the quasi-Monte Carlo method
ans =
0.7853
In this instance (and this will be true for many problems), quasirandom numbers have converged faster.
See also the Mar-19-2008 posting, Quasi-Random Numbers. As mentioned in that post, coordinates of a regular grid could be substituted for the random or quasirandom numbers, but this requires knowing in advance how many samples are to be drawn, and does not allow arbitrary amounts of further sampling to be used to improve the approximation.
Naturally, one would never bother with all of this to calculate the area of a circle, given the availability of convenient formula, but Monte Carlo can be used for regions of arbitrary, possibly highly irregular- even disjoint- regions. As with the bootstrap, simulated annealing and genetic algorithms, this method is made possible by the fact that modern computers provide tremendous amounts of rapid, accurate computation at extremely low cost.
Further Reading
For a good overview of the Monte Carlo method, see:
Monte Carlo Method
Wednesday, March 19, 2008
Quasi-Random Numbers
Many computer users, whether MATLAB programmers or not, are familiar with random numbers. Strictly speaking, the "random" numbers most often encountered on computers are known as pseudo-random numbers. Pseudo-random numbers are not actually "random" at all, as they are deterministically generated in a completely repeatable fashion using one of a number of algorithms called pseudo-random number generators ("PRNG", if you want to impress your friends with lingo). Pseudo-random numbers are designed to mimic specific statistical distributions, most often the uniform distribution or, somewhat less commonly, the normal distribution.
The usefulness of random (or pseudo-random) numbers cannot be overestimated. They are used in computers for such different purposes as optimization, numerical integration, machine learning, simulation and scheduling. A common theme among these applications is the utilization of random numbers to cover or search a geometric space, most often accomplished via uniformly distributed random numbers. In such cases, sets of random numbers define the coordinates of single points in the searched space.
As a simplified example, think of a petroleum company searching for oil in a square plot of land. With no knowledge of where the oil may lie, and a limited budget for drilling holes, the company requires some method for selecting locations to test. Uniformly distributed random numbers could be used for this purpose, but they present a subtle deficiency, informally known as "clumping". Since each coordinate pair is drawn completely independently and the random numbers being used are uncorrelated with one another, there is the real possibility that test sites will be specified near existing test sites. One would imagine that new test sites within our square should be as far as possible from sites already tested. Whether existing sites are dry or not, testing very near them would seem to add little information.
Perhaps a better choice in such circumstances would be quasi-random numbers. Quasi-random numbers behave something like random numbers, but are generated as correlated vectors, so as to better obey the intended distribution, even in multiple dimensions. In our oil drilling problem, quasi-random numbers could be generated in pairs to form coordinates for drilling sites. Such coordinates would be less likely to fall near those already generated. Quasi-random numbers are known to converge to a solution faster than random ones in a variety of problems, such as numeric integration.
The following scatter plots illustrate the difference between the two (click to enlarge):
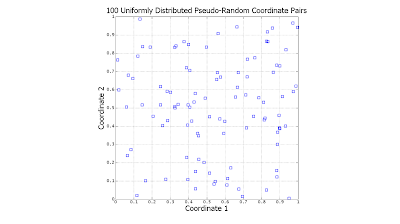
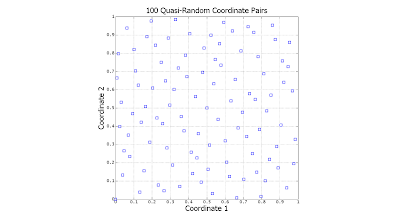
Notice the significant gaps left by the random data. There is nothing "wrong" with this: However undesirable, this is exactly how uniformly-distributed random data is expected to behave. In contrast, the quasi-random data is much more evenly distributed.
At this point, a question which might logically occur to the reader is, "Why not simply search on a regularly-spaced grid?" Grid searching is certainly a viable alternative, but requires that one know ahead of time precisely how many coordinates need to be generated. If the oil company in our example searches over a grid and discovers later that it has the budget for less or more tests than it originally planned, then the grid search will be sub-optimal. One very convenient property of quasi-random numbers is that however few or many are generated, they will (more-or-less) spread out as evenly as possible.
Clever as they are, most readers will be familiar with the pseudo-random number generators provided in base MATLAB, rand and randn. See, for instance the posts:
Dec-07-2006: Quick Tip Regarding rand and randn
Jan-13-2007: Revisiting rand (MATLAB 2007a)
Mar-23-2008: A Quick Introduction to Monte-Carlo and Quasi-Monte Carlo Integration
Quasi-random number generation is a recent addition to the MATLAB Statistics Toolbox (as of v6.2). The relevant functions are qrandstream, sobolset (Sobol generator) and haltonset (Halton generator). Other quasi-random number code can also be found for free via on-line searching (see the Nov-14-2006 post, Finding MATLAB Source Code And Tools). To research this subject further, look for material on "low discrepancy" sequences (the more technical name for quasi-random numbers).
The usefulness of random (or pseudo-random) numbers cannot be overestimated. They are used in computers for such different purposes as optimization, numerical integration, machine learning, simulation and scheduling. A common theme among these applications is the utilization of random numbers to cover or search a geometric space, most often accomplished via uniformly distributed random numbers. In such cases, sets of random numbers define the coordinates of single points in the searched space.
As a simplified example, think of a petroleum company searching for oil in a square plot of land. With no knowledge of where the oil may lie, and a limited budget for drilling holes, the company requires some method for selecting locations to test. Uniformly distributed random numbers could be used for this purpose, but they present a subtle deficiency, informally known as "clumping". Since each coordinate pair is drawn completely independently and the random numbers being used are uncorrelated with one another, there is the real possibility that test sites will be specified near existing test sites. One would imagine that new test sites within our square should be as far as possible from sites already tested. Whether existing sites are dry or not, testing very near them would seem to add little information.
Perhaps a better choice in such circumstances would be quasi-random numbers. Quasi-random numbers behave something like random numbers, but are generated as correlated vectors, so as to better obey the intended distribution, even in multiple dimensions. In our oil drilling problem, quasi-random numbers could be generated in pairs to form coordinates for drilling sites. Such coordinates would be less likely to fall near those already generated. Quasi-random numbers are known to converge to a solution faster than random ones in a variety of problems, such as numeric integration.
The following scatter plots illustrate the difference between the two (click to enlarge):


Notice the significant gaps left by the random data. There is nothing "wrong" with this: However undesirable, this is exactly how uniformly-distributed random data is expected to behave. In contrast, the quasi-random data is much more evenly distributed.
At this point, a question which might logically occur to the reader is, "Why not simply search on a regularly-spaced grid?" Grid searching is certainly a viable alternative, but requires that one know ahead of time precisely how many coordinates need to be generated. If the oil company in our example searches over a grid and discovers later that it has the budget for less or more tests than it originally planned, then the grid search will be sub-optimal. One very convenient property of quasi-random numbers is that however few or many are generated, they will (more-or-less) spread out as evenly as possible.
Clever as they are, most readers will be familiar with the pseudo-random number generators provided in base MATLAB, rand and randn. See, for instance the posts:
Dec-07-2006: Quick Tip Regarding rand and randn
Jan-13-2007: Revisiting rand (MATLAB 2007a)
Mar-23-2008: A Quick Introduction to Monte-Carlo and Quasi-Monte Carlo Integration
Quasi-random number generation is a recent addition to the MATLAB Statistics Toolbox (as of v6.2). The relevant functions are qrandstream, sobolset (Sobol generator) and haltonset (Halton generator). Other quasi-random number code can also be found for free via on-line searching (see the Nov-14-2006 post, Finding MATLAB Source Code And Tools). To research this subject further, look for material on "low discrepancy" sequences (the more technical name for quasi-random numbers).
Labels:
discrepancy,
Gaussian,
low discrepancy,
normal,
PRNG,
pseudo-random,
pseudorandom,
quasi-random,
quasirandom,
random,
uniform
Sunday, March 16, 2008
MATLAB 2008a Released
While not on disk yet, MATLAB release 2008a (MATLAB 7.6) is available for download from the MathWorks for licensed users. This release brings news on several fronts:
The Statistics Toolbox has seen a number of interesting additions, including: quasirandom number generators and (sequential) feature selection and cross-validation for modeling functions.
Another change which may be of interest to readers of this log is the upgrade of the Distributed Computing Toolbox, now named the Parallel Computing Toolbox. This Toolbox permits (with slight restructuring of MATLAB code) the distribution of the computational workload over multiple processors or processor cores. With more and more multi-core computers being sold every month, this offers the opportunity to greatly accelerate MATLAB code execution (think in terms of multiples of performance, not mere percentages!) to a very broad audience. Code which can be parallelized will run nearly twice as fast on a dual-core machine, and nearly four times as fast on a quad-core machine.
On a non-technical note, MATLAB has finally moved beyond software keys to on-line authentication for software installation. Is this good or bad? Both, I suppose. I'm sure that the MathWorks experiences its share of software piracy, so this move is understandable. It's also worth mentioning that MATLAB licensing is still very casual, with "one user" licensing still permitting installation on multiple machines (such as work and home), with the understanding that only one licensed person will use the software at a time.
The Statistics Toolbox has seen a number of interesting additions, including: quasirandom number generators and (sequential) feature selection and cross-validation for modeling functions.
Another change which may be of interest to readers of this log is the upgrade of the Distributed Computing Toolbox, now named the Parallel Computing Toolbox. This Toolbox permits (with slight restructuring of MATLAB code) the distribution of the computational workload over multiple processors or processor cores. With more and more multi-core computers being sold every month, this offers the opportunity to greatly accelerate MATLAB code execution (think in terms of multiples of performance, not mere percentages!) to a very broad audience. Code which can be parallelized will run nearly twice as fast on a dual-core machine, and nearly four times as fast on a quad-core machine.
On a non-technical note, MATLAB has finally moved beyond software keys to on-line authentication for software installation. Is this good or bad? Both, I suppose. I'm sure that the MathWorks experiences its share of software piracy, so this move is understandable. It's also worth mentioning that MATLAB licensing is still very casual, with "one user" licensing still permitting installation on multiple machines (such as work and home), with the understanding that only one licensed person will use the software at a time.
Saturday, March 01, 2008
An Update on the Status of this Web Log
Four calendar months have elapsed with no technical update to this Web log. Judging by visitation statistics, though, this log is more popular than ever, ironically enough.
I do very much appreciate the kind words which appear from readers in the comments sections and in private communication. This Web log will continue to be updated, though for personal reasons, perhaps less frequently.
I do very much appreciate the kind words which appear from readers in the comments sections and in private communication. This Web log will continue to be updated, though for personal reasons, perhaps less frequently.
Subscribe to:
Comments (Atom)