Quasi-Random Numbers

Many computer users, whether MATLAB programmers or not, are familiar with random numbers. Strictly speaking, the "random" numbers most often encountered on computers are known as pseudo-random numbers. Pseudo-random numbers are not actually "random" at all, as they are deterministically generated in a completely repeatable fashion using one of a number of algorithms called pseudo-random number generators ("PRNG", if you want to impress your friends with lingo). Pseudo-random numbers are designed to mimic specific statistical distributions, most often the uniform distribution or, somewhat less commonly, the normal distribution.

The usefulness of random (or pseudo-random) numbers cannot be overestimated. They are used in computers for such different purposes as optimization, numerical integration, machine learning, simulation and scheduling. A common theme among these applications is the utilization of random numbers to cover or search a geometric space, most often accomplished via uniformly distributed random numbers. In such cases, sets of random numbers define the coordinates of single points in the searched space.

As a simplified example, think of a petroleum company searching for oil in a square plot of land. With no knowledge of where the oil may lie, and a limited budget for drilling holes, the company requires some method for selecting locations to test. Uniformly distributed random numbers could be used for this purpose, but they present a subtle deficiency, informally known as "clumping". Since each coordinate pair is drawn completely independently and the random numbers being used are uncorrelated with one another, there is the real possibility that test sites will be specified near existing test sites. One would imagine that new test sites within our square should be as far as possible from sites already tested. Whether existing sites are dry or not, testing very near them would seem to add little information.

Perhaps a better choice in such circumstances would be quasi-random numbers. Quasi-random numbers behave something like random numbers, but are generated as correlated vectors, so as to better obey the intended distribution, even in multiple dimensions. In our oil drilling problem, quasi-random numbers could be generated in pairs to form coordinates for drilling sites. Such coordinates would be less likely to fall near those already generated. Quasi-random numbers are known to converge to a solution faster than random ones in a variety of problems, such as numeric integration.

The following scatter plots illustrate the difference between the two (click to enlarge):





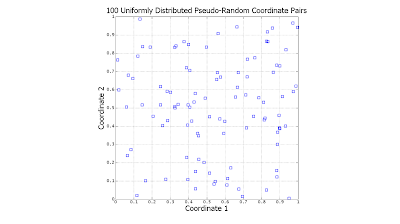
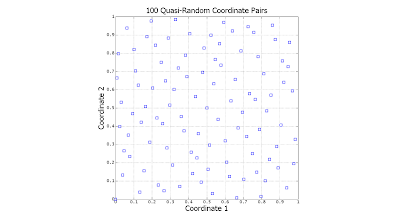
Notice the significant gaps left by the random data. There is nothing "wrong" with this: However undesirable, this is exactly how uniformly-distributed random data is expected to behave. In contrast, the quasi-random data is much more evenly distributed.

At this point, a question which might logically occur to the reader is, "Why not simply search on a regularly-spaced grid?" Grid searching is certainly a viable alternative, but requires that one know ahead of time precisely how many coordinates need to be generated. If the oil company in our example searches over a grid and discovers later that it has the budget for less or more tests than it originally planned, then the grid search will be sub-optimal. One very convenient property of quasi-random numbers is that however few or many are generated, they will (more-or-less) spread out as evenly as possible.

Clever as they are, most readers will be familiar with the pseudo-random number generators provided in base MATLAB, rand and randn. See, for instance the posts:

Dec-07-2006: Quick Tip Regarding rand and randn
Jan-13-2007: Revisiting rand (MATLAB 2007a)
Mar-23-2008: A Quick Introduction to Monte-Carlo and Quasi-Monte Carlo Integration

Quasi-random number generation is a recent addition to the MATLAB Statistics Toolbox (as of v6.2). The relevant functions are qrandstream, sobolset (Sobol generator) and haltonset (Halton generator). Other quasi-random number code can also be found for free via on-line searching (see the Nov-14-2006 post, Finding MATLAB Source Code And Tools). To research this subject further, look for material on "low discrepancy" sequences (the more technical name for quasi-random numbers).